10 Overlevelsesanalyse
Eksempel: Lungecancer uge 9.
Se også forelæsningerne i Introduktion til overlevelsesanalyse uge 9 (find link fra forside på Absalon), hvor der ligger nogle videoer om overlevelsesanalyse i R.
I en overlevelsesanalyse består outcome-variablen af to elementer:
- En variabel der beskriver overlevelsestiden (her
time) - En variabel der beskriver om observationen af overlevelsestiden er et event/dødsfald eller en censurering (her
status)
Afhængigt af hvilken pakke / funktioner man bruger skal man klistre disse to variable sammen i et survival-outcome med
Surv(time, status)hvis funktioner frasurvivalellertimereg-pakken benyttes.Hist(time,status)hvis funktioner fraprodlim-pakken benyttes.
Det er selvfølgelig lidt besværligt at man skal angive sit outcome forskelligt afhængigt af hvilken pakke man bruger - men vi bruger her kun prodlim-pakken til at tegne lidt pænere Kaplan-Meier kurver, så udgangspunktet er at vi skal angive outcome som Surv(time,status) (og gør vi det galt, skal R nok brokke sig …).
10.1 Kaplan-Meier kurver
For at lave Kaplan-Meier kurver kan man enten benytte funktionen survfit() fra survival-pakken eller prodlim() fra prodlim-pakken og herefter benytte funktionen plot().
Benyttes prodlim() tilføjes der automatisk konfidenslinjer. Benyttes survfit() er det også muligt at tilføje konfidenslinjer ved at angive conf.int=T i plot()-funktionen, men figuren bliver ikke lige så pæn som ved prodlim().
library( survival )
km1 <- survfit( Surv(time, status) ~ treat, data=d )
plot( km1 )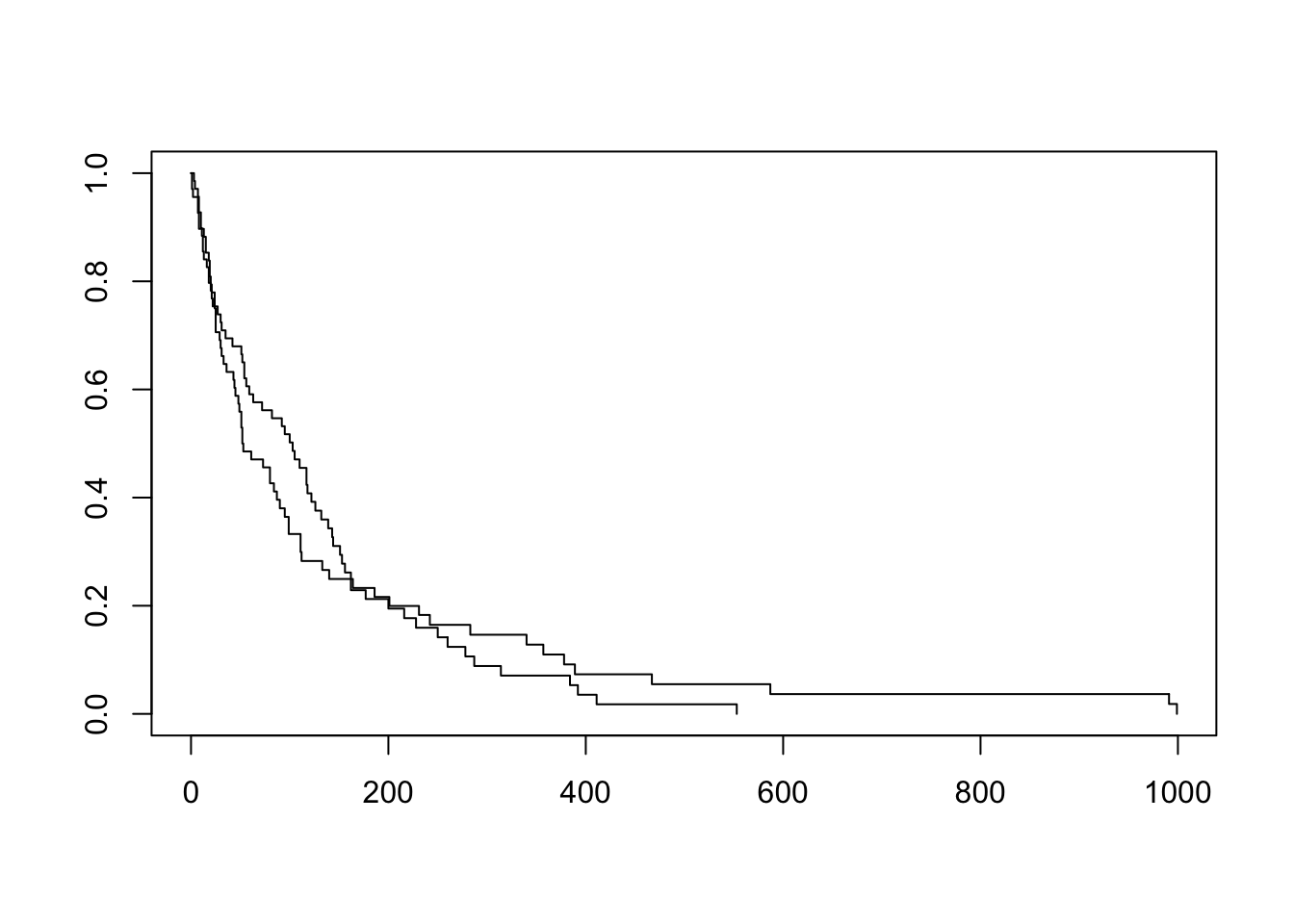
library(prodlim)
km2 <- prodlim( Hist(time, status) ~ treat, data=d )
plot( km2 )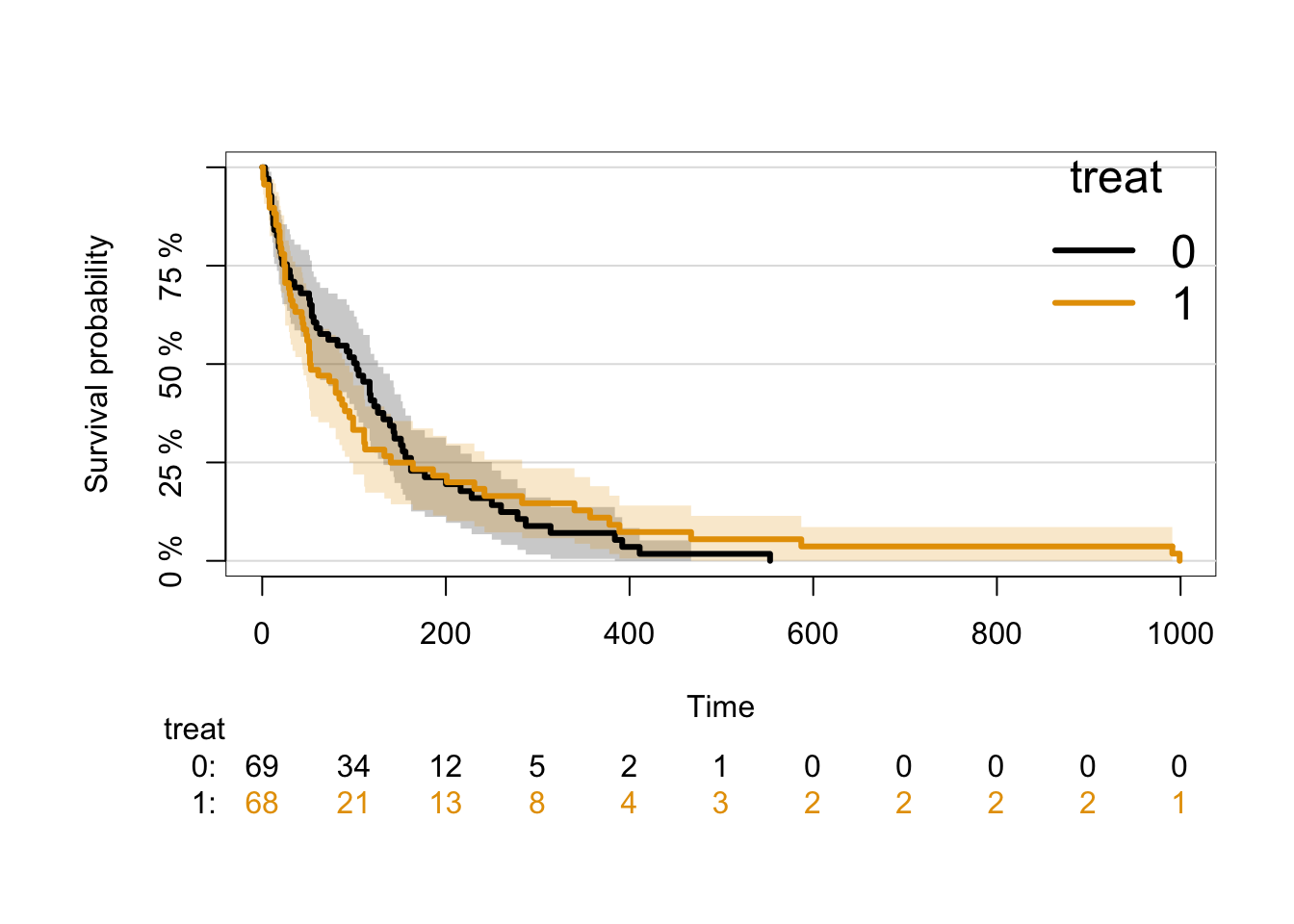
10.1.1 Kumulative incidenser
For at plotte kumulativ incidens kan man igen benytte plot() på et prodlim-objekt, men nu med argument type = "cuminc".
plot( km2, type = "cuminc")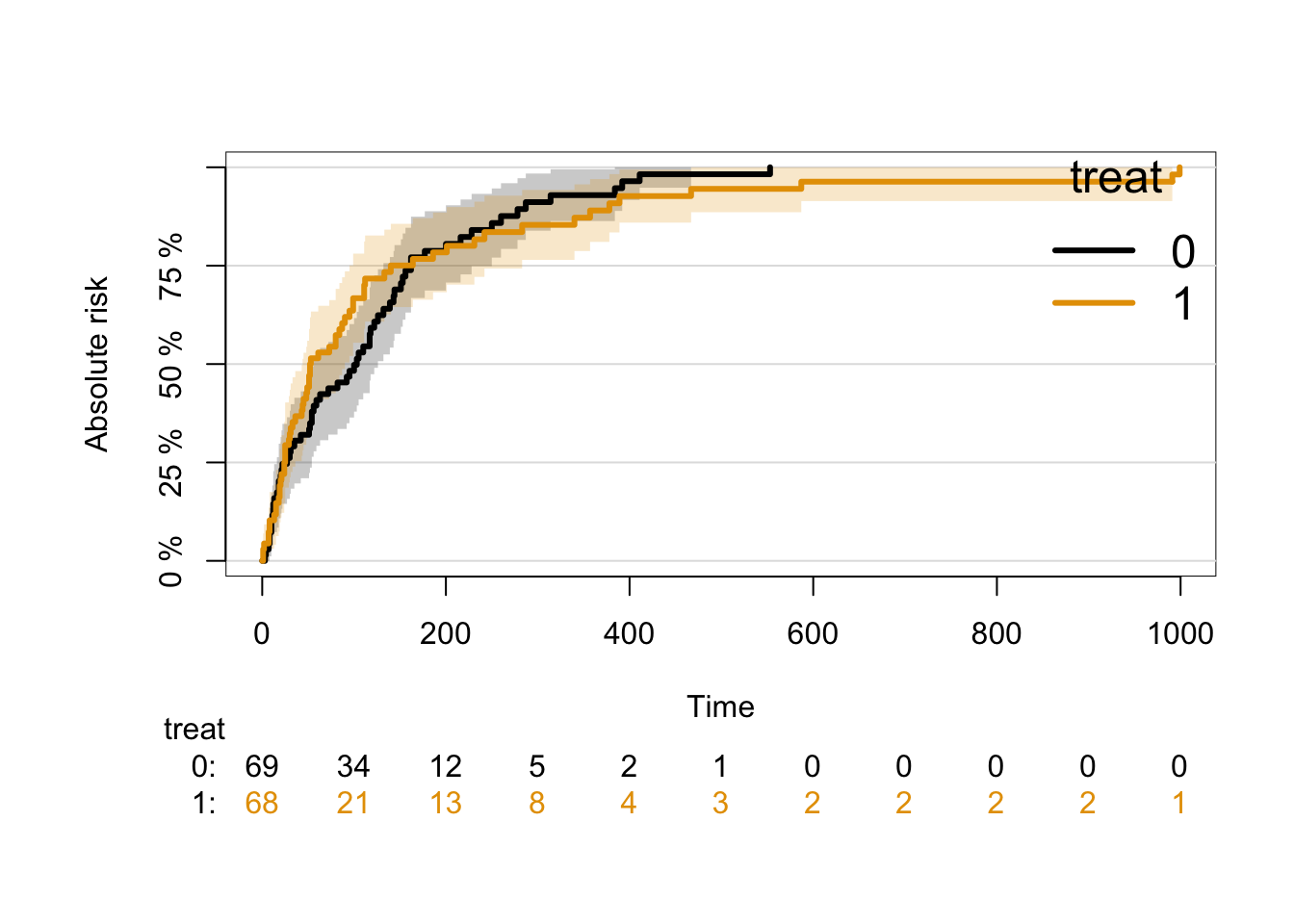
10.1.2 Kumulerede hazard funktioner
Vi plotter de kumulerede hazard funktioner som funktion af tid, og vurderer om kurverne er proportionale da vi i så fald har proportionale hazards og kan fortsætte med en Cox-regression.
Her angiver vi fun = "cumhaz". For at give kurverne forskellige farver tiltøjes col = 1:2, da der er to grupper. Derefter kan vi tilføje en forklaring til figuren med legend-funktionen.
plot( km1, fun = "cumhaz", col = 1:2 )
legend( "bottomright", c("0","1"), inset = .01, title = "Treatment", lty = 1, col = 1:2)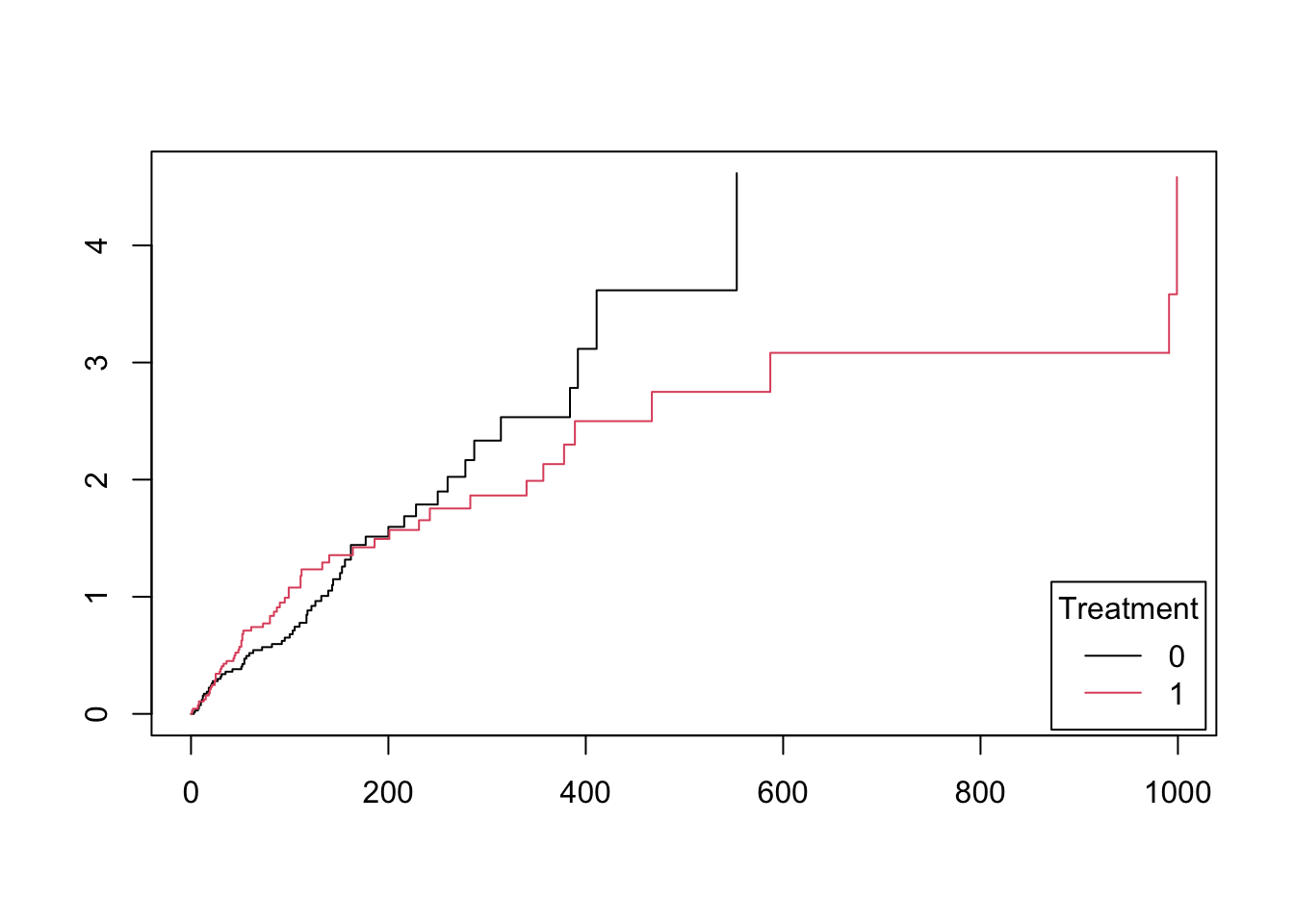
10.1.3 Log-rank test
Log-rank testet bruges til at teste, om overlevelseskurverne er ens. Hertil benyttes survdiff-functionen.
P-værdien aflæses nederst i outputtet (p= 0.90, dvs der er ikke tegn på at kurverne er forskellige)
survdiff( Surv(time, status) ~ treat, data = d)Call:
survdiff(formula = Surv(time, status) ~ treat, data = d)
N Observed Expected (O-E)^2/E (O-E)^2/V
treat=0 69 64 64.5 0.00388 0.00823
treat=1 68 64 63.5 0.00394 0.00823
Chisq= 0 on 1 degrees of freedom, p= 0.9 10.2 Cox proportional hazards model
For at opstille en Cox Proportional Hazards model benyttes funktionen coxph().
Som i en lineær model med lm-funktionen angives relationen mellem outcome (Surv(time, status)) og kovariater som en formel, hvor ~ adskiller outcome fra kovariater, og kovariater tilføjes med +, dvs.
\[\text{outcome} \sim \text{kovariat1} + \text{kovariat2} + \text{kovariat3}\]
Interaktioner mellem kovariater kan angives i formlen med * eller : som vi plejer.
Nedenfor angiver vi en Cox Proportional Hazards model med treat, celltype og karno som kovariater uden interaktioner.
cox.mod1 <- coxph( Surv(time, status) ~ factor(treat) + celltype + karno,
data = d )Parameterestimater fås derefter med summary()-funktionen. Estimater for hazard-ratio aflæses under exp(coef) og konfidensintervaller for exp(coef) aflæses under lower .95 og upper .95. P-værdien aflæses under Pr(>|z|)
summary( cox.mod1 )Her er summary() så venlig også at beregne CI for os, så vi behøver ikke at benytte confint() (som dog også virker her).
10.2.1 Test
Overordnet test for association for hver variabel i en Cox model, kan laves med drop1(), hvor vi angiver Cox modellen samt test = "Chisq".
drop1( cox.mod1, test = "Chisq")Single term deletions
Model:
Surv(time, status) ~ factor(treat) + celltype + karno
Df AIC LRT Pr(>Chi)
<none> 960
factor(treat) 1 960 1.7 0.19263
celltype 3 972 18.1 0.00042 ***
karno 1 993 35.2 3e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vi kan teste hypoteser om flere parametre i en Cox model simultant vha. linearHypothesis-funktionen fra car-pakken. Her angives Cox modellen samt hypoteserne, der skal testes. I eksemplet nedenfor tester vi om koefficienterne hørende til large, smallcell og squamous for variablen celltype alle er 0 (et test med 3 frihedsgrader da vi sætter 3 koefficienter til 0). Dette er altså det samme som det overordnede test for effekt af celltype, men man får en lidt anden p-værdi fordi der benyttes en anden metode til beregning af p-værdien
library(car)
linearHypothesis( cox.mod1, c("celltypelarge = 0",
"celltypesmallcell = 0",
"celltypesquamous = 0"))Linear hypothesis test
Hypothesis:
celltypelarge = 0
celltypesmallcell = 0
celltypesquamous = 0
Model 1: restricted model
Model 2: Surv(time, status) ~ factor(treat) + celltype + karno
Res.Df Df Chisq Pr(>Chisq)
1 135
2 132 3 17.5 0.00056 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 110.2.2 Modelkontrol: Proportional Hazards
For alle kovariater skal antagelsen om proportional hazards tjekkes. Det kan gøres grafisk såvel som ved et test.
Nedenfor beskrives først den ‘gammeldags’ metode, som kan benyttes for kvalitative forklarende variable (kvantitative kan checkes på tilsvarende vis ved inddeling af den kvantative kovariat i grupper).
Dernæst beskrives en mere moderne metode baseret på de såkaldte Score-residualer. Denne metode kan benyttes på både kvantitative og kvalitative variable.
10.2.2.1 Kvalitative forklarende variable
Man kan lave en grafisk kontrol af antagelse om proportionale hazards mellem grupper for en kvalitativ variabel ved at tjekke parallelitet af de kumulerede hazard-funktioner på loglog-skala.
Dette kan gøres på følgende måde:
Først fittes en coxph-model, hvor variablen, vi ønsker at tjekke proportionale hazards for, sættes i strata() (se kode nedenfor).
Hvis der er øvrige kovariater i modellen ud over variablen i strata, laver vi et datasæt med en enkelt, vilkårlig værdi af hver af disse variabler. Dette gøres med data.frame().
Hernæst laver vi et surfit-objekt med surfit()-funktionen. Her angiver vi vores Cox model, samt det nye datasæt i newdata =.
Dette survfit-objekt kan vi benytte til at lave plot af kumumlerede hazard funktioner på loglog-skala med plot()-funktionen, hvor vi angiver fun = "cloglog".
I eksemplet nedenfor har vi valgt at tjekke proportional hazards mellem grupperne i variablen treat. Proceduren gentages for de øvrige kvalitative variable en af gangen, hvor disse angives i strata.
cox.mod2 <- coxph( Surv(time,status) ~ strata(treat) + celltype + karno, data = d )
newD = data.frame( celltype = "squamous", karno = 50) # Vaelg vilkaarlig vaerdi for celltype og karno
survfit2 = survfit( cox.mod2, newdata = newD )
plot( survfit2, fun = "cloglog", ylab = "log(-log(S))", col = 1:2, xlab = "time")
legend("bottomright", c("0","1"), lty = 1, col = 1:2, title = "Treatment", inset = .01)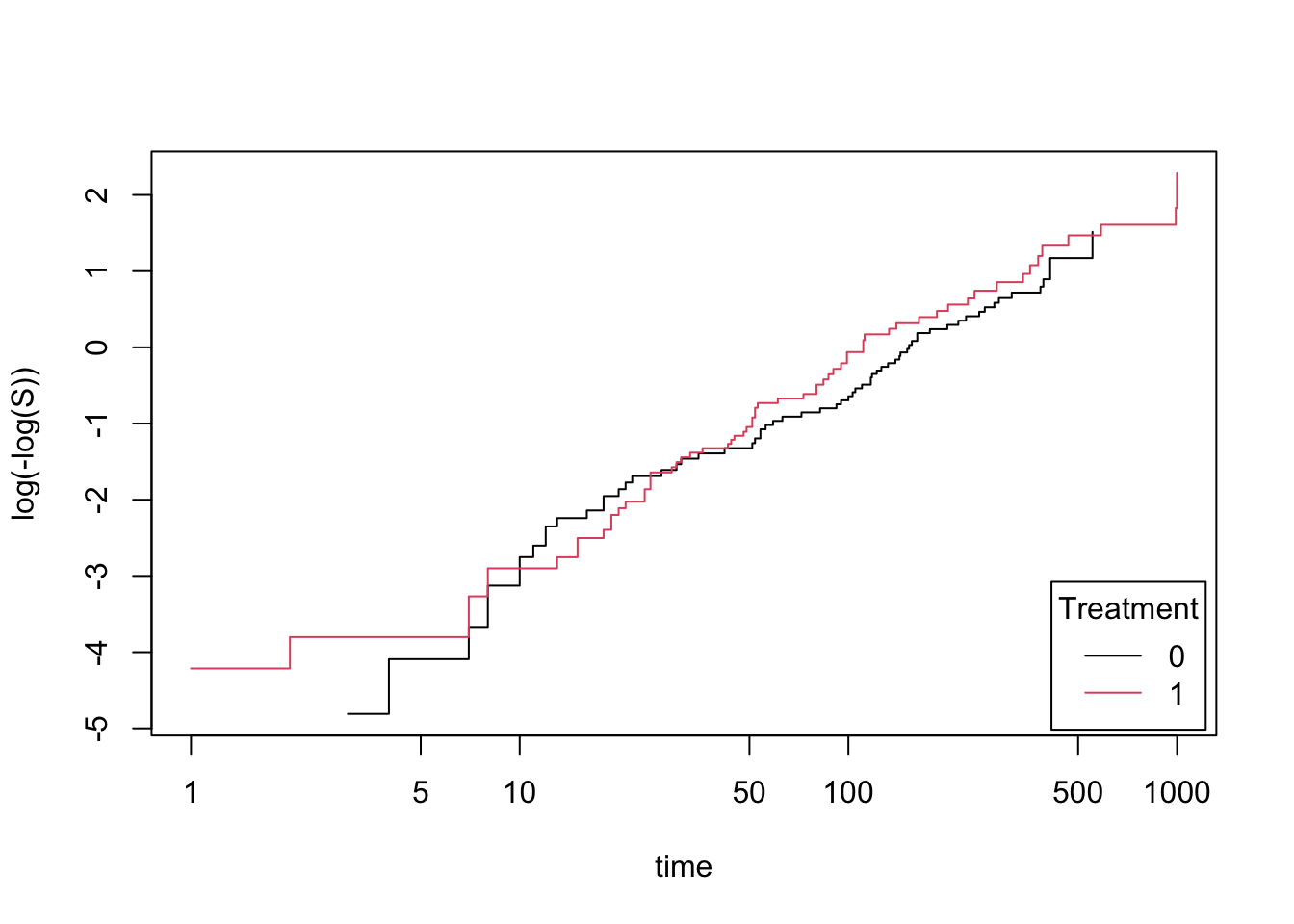
10.2.2.2 Kvalitative og kvantitative kovariater
En anden måde at tjekke proportionale rater grafisk er vha. Score-residualer. Til dette benytter vi cox.aalen()-funktionen i timreg-pakken.
I cox.aalen() skal alle kovariater med antagelse om proportionalitet angives i prop() (se kode nedenfor).
Med plot() kan vi plotte de kumulerede Score-residualer ved at angive score=T. Derved får ét plot for hver parameter med antagelse om proportionalitet i modellen. Ved at angive specific.comps =, kan man kontrollere hvilke af figurerne, man vil have vist.
Da cox.aalen() benytter nogle tilfældige simulationer, kan vi sikre, at vi får samme resultat, hver gang vi kører funktionen på den samme model, ved at angive et såkald seed i set.seed(). Her angives et tilfældigt tal. Hver gang set.seed() køres inden cox.aalen, får man så det samme resultat. Her skal man vurdere, om den sorte (observerede) kurve stemmer overens med de grå (simulerede) kurver.
library( timereg )
set.seed( 123 ) # Valgfrit tal
par(mfrow=c(3,2))
ca1 <- cox.aalen( Surv(time,status) ~ prop( factor(treat)) + prop(celltype) + prop(karno), data = d)
plot( ca1, score = T )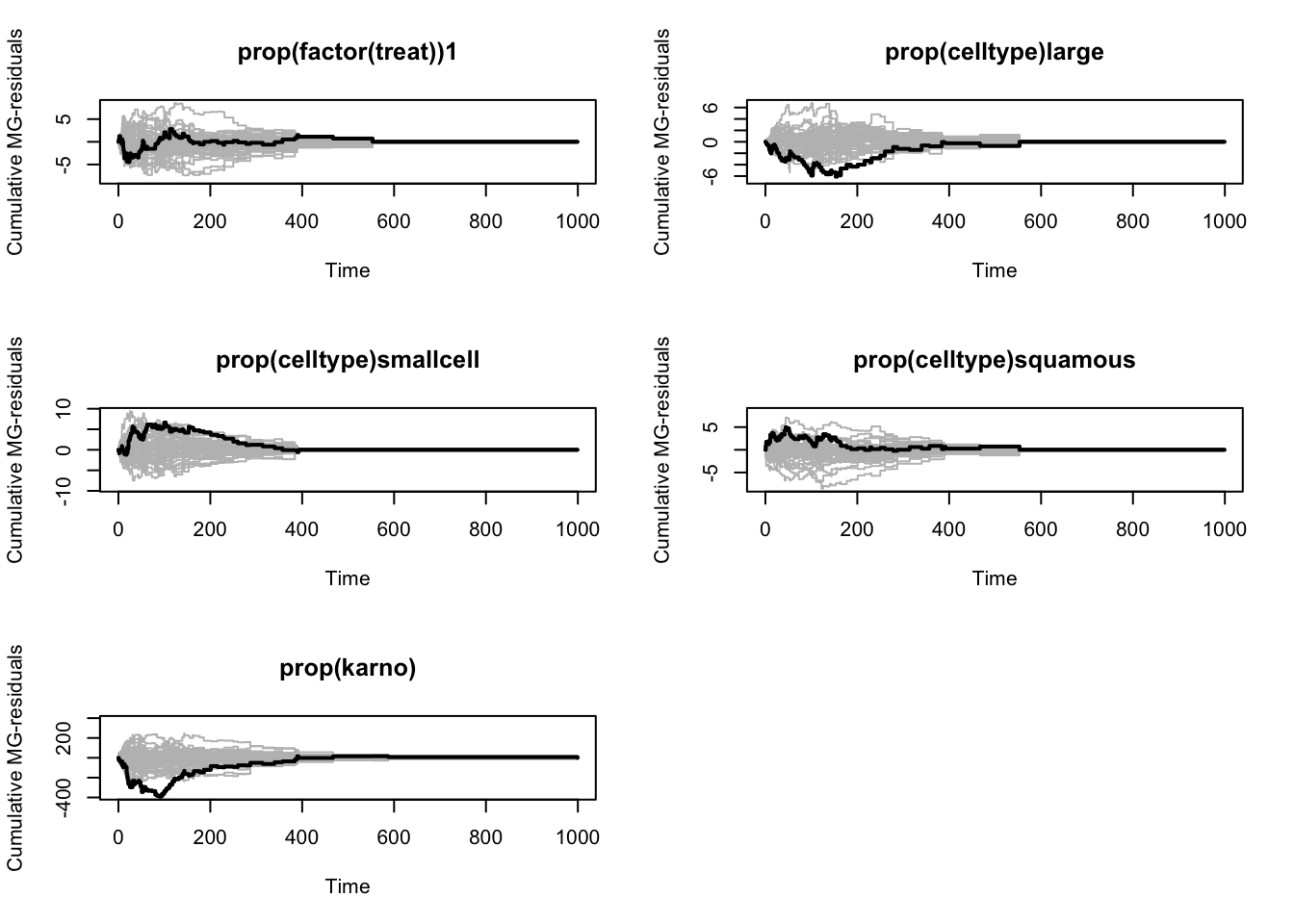
Som en hjælp til at vurdere, om proportional hazards er opfyldt kan vi få en p-værdi frem ved at benytte summary() på cox.aalen modellen defineret ovenfor.
P-værdier aflæses under p-value H_0.
summary( ca1 )I princippet kan vi klare os med p-værdierne for at vurdere proportional hazards antagelsen - men det er en god idé at se på plottene for at få en idé om, hvor en eventuel afvigelse er.
10.2.3 Modelkontrol: Linearitet
Antagelsen om linearitet på log-hazard skala kan tjekkes ved brug af kumulerede martingal residualer. Martingal residualerne fås ved at lave en cox.aalen-model, hvor vi angiver residuals=1 og n.sim=0.
Hernæst benyttes cum.residuals() med cum.resid=1 for at få de kumulerede residualer.
Test for ikke-linearitet laves da vha. summary() og aflæses under p-value H_0: B(t)=0.
set.seed( 345 )
ca3 <- cox.aalen( Surv(time,status) ~ prop(factor(treat)) + prop(celltype) + prop(karno),
data=d, residuals=1, n.sim=0 )
resids <- cum.residuals( ca3, cum.resid=1, data=d )
summary(resids)Desuden kan vi plotte residualerne ved at sætte score=2
plot( resids, score=2 )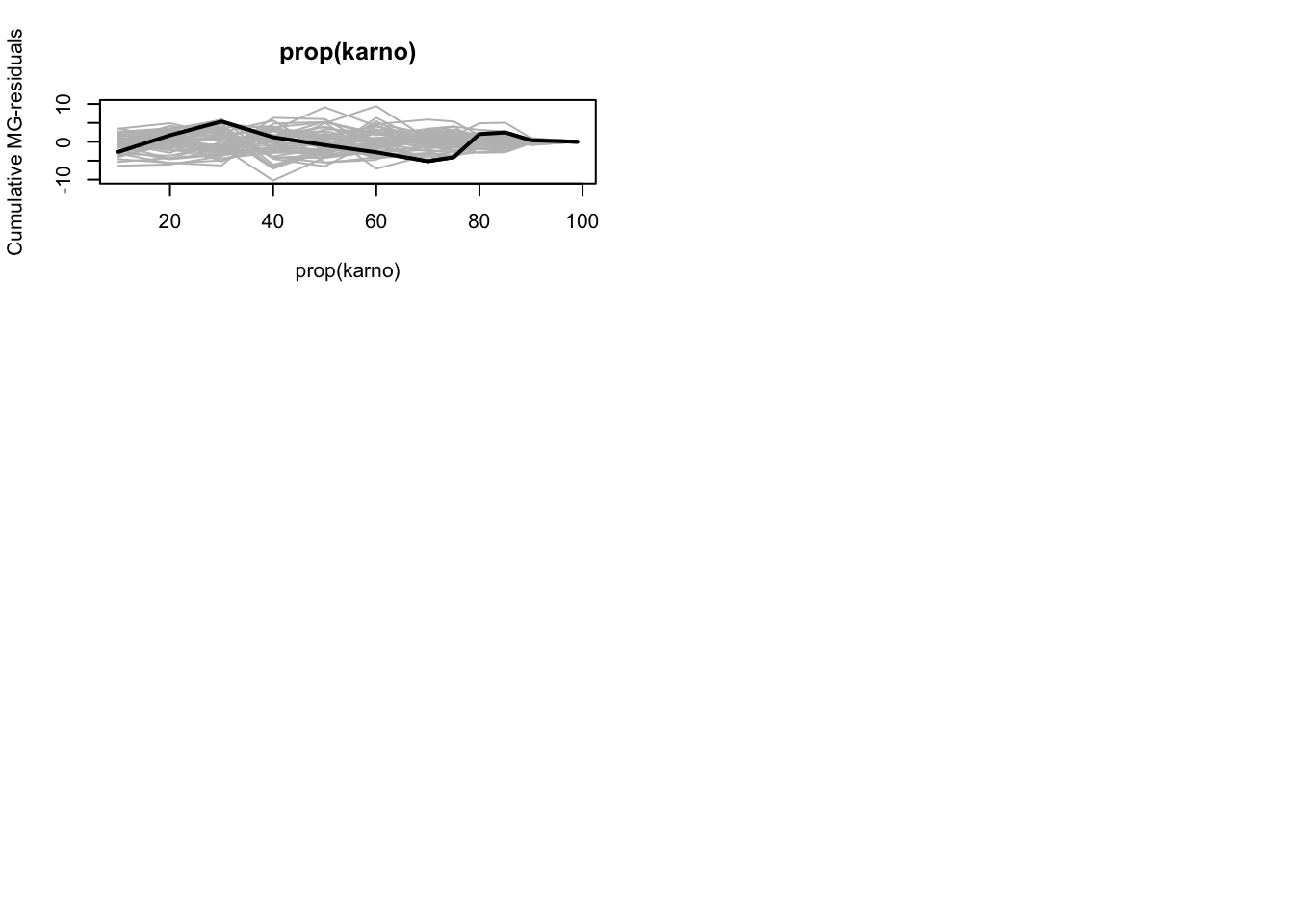
10.2.4 Tidsafhængige kovariater
I en Cox proportional hazards model (coxph()) er det muligt at lade effekten af en variabel ændre sig over tid.
I formellinjen sættes tt() omkring den variabel, der skal afhænge af tiden, og selve tidstransformationen variablen angives i argumentet tt= som en funktion (tt = function(k,t,...){}). Her repræsenterer k variablen, der afhænger af tiden, og t repræsenterer tid.
I eksemplet nedenfor lader vi effekten kovariaten karno være opdelt i 4 tidsintervaller (\(t\leq23\), \(t\in(23,62]\), \(t\in(62,147.5]\) og \(t>147.5\)). Det betyder altså, at vi skal rapportere fire forskellige HR’er - en for hvert tidsinterval.
I funktionsudtrykket i tt=, laver vi med cbind() en vektor med 4 indgange, hvor hver indgang tager værdien \(k\), netop hvis \(t\) er i det interval, som svarer til den indgang, og ellers antager den værdien 0. Det skyldes at fx. (t<=23)=1 hvis \(t\leq23\) og 0 ellers, og derfor er k*(t<=23) = k hvis \(t\leq23\) og 0 ellers.
Der kan derfor kun være én indgang ad gangen, der er forskellig fra 0. På den måde opdeles effekten af karno i 4 tidsintervaller.
I summary() på modellen kan vi se, at der er 4 parametre for tt(karno) svarende til en for hvert tidsinterval.
cox.mod3 <- coxph( Surv(time,status) ~ factor(treat) + celltype + tt(karno),
data = d,
tt = function(k, t, ...) { cbind( k*(t<=23),
k*(t>23 & t<=62),
k*(t>62 & t<=147.5),
k*(t>147.5)) }
)
summary(cox.mod3)Call:
coxph(formula = Surv(time, status) ~ factor(treat) + celltype +
tt(karno), data = d, tt = function(k, t, ...) {
cbind(k * (t <= 23), k * (t > 23 & t <= 62), k * (t > 62 &
t <= 147.5), k * (t > 147.5))
})
n= 137, number of events= 128
coef exp(coef) se(coef) z Pr(>|z|)
factor(treat)1 0.08422 1.08787 0.20516 0.41 0.68143
celltypelarge -0.76177 0.46684 0.30110 -2.53 0.01141 *
celltypesmallcell -0.21004 0.81055 0.26795 -0.78 0.43311
celltypesquamous -1.09673 0.33396 0.30059 -3.65 0.00026 ***
tt(karno)1 -0.05179 0.94953 0.00928 -5.58 2.4e-08 ***
tt(karno)2 -0.03656 0.96410 0.00911 -4.01 6.0e-05 ***
tt(karno)3 -0.00770 0.99233 0.01218 -0.63 0.52756
tt(karno)4 -0.00310 0.99691 0.01284 -0.24 0.80920
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
factor(treat)1 1.088 0.919 0.728 1.626
celltypelarge 0.467 2.142 0.259 0.842
celltypesmallcell 0.811 1.234 0.479 1.370
celltypesquamous 0.334 2.994 0.185 0.602
tt(karno)1 0.950 1.053 0.932 0.967
tt(karno)2 0.964 1.037 0.947 0.981
tt(karno)3 0.992 1.008 0.969 1.016
tt(karno)4 0.997 1.003 0.972 1.022
Concordance= 0.752 (se = 0.023 )
Likelihood ratio test= 74.7 on 8 df, p=6e-13
Wald test = 73.5 on 8 df, p=1e-12
Score (logrank) test = 82.5 on 8 df, p=2e-14